Rethinking B-tree block sizes on SSDs
One of the first questions to answer when running databases on SSDs is what B-tree block size to use. There are a number of factors that affect this decision:
- The type of workload
- I/O time to read and write the block size
- The size of the cache
That’s a lot of variables to consider. For this blog post we assume a fairly common OLTP scenario - a database that’s dominated by random point queries. We will also sidestep some of the more subtle caching effects by treating the caching algorithm as perfectly optimal, and assuming the cost of lookup in RAM is insignificant.
Even with these restrictions it isn’t immediately obvious what is the optimal block size. Before discussing SSDs, let’s quickly address this problem on rotational drives. If we benchmark the number of IOPS for different block sizes on a typical rotation drive we get the following graph:
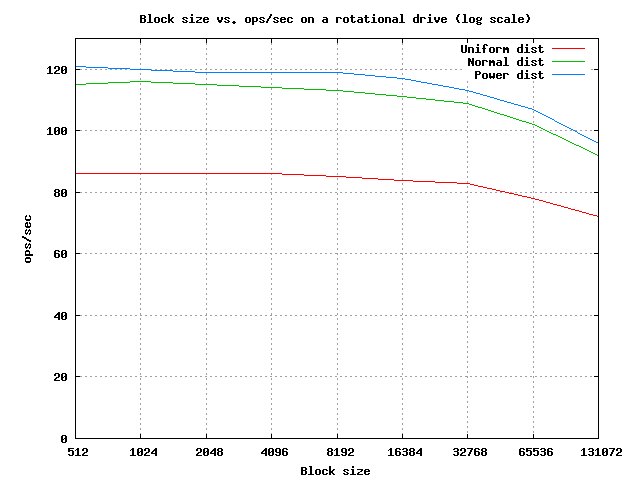
There are two things to note. The first, is that the random distribution makes a big difference, resulting in a 25% speedup between uniform and power distributions. The curves, however, are roughly the same, which means that ignoring caching, the ideal block size isn’t dependent on the distribution. The second, is that the number of IOPS is effectively constant for all blocks before 16KB. This is supported by the assumption that the time it takes to read extra information once the arm is properly positioned is insignificant compared to the seek latency and rotational delays. So, for a rotational drive, I/O read time changes are not a significant factor - we should design the block size completely based on the caching effects. But what about solid state drives?
The first natural thing to do is to benchmark the number of IOPS for different block sizes. A couple of runs of Rebench fed into gnuplot give us the following results:
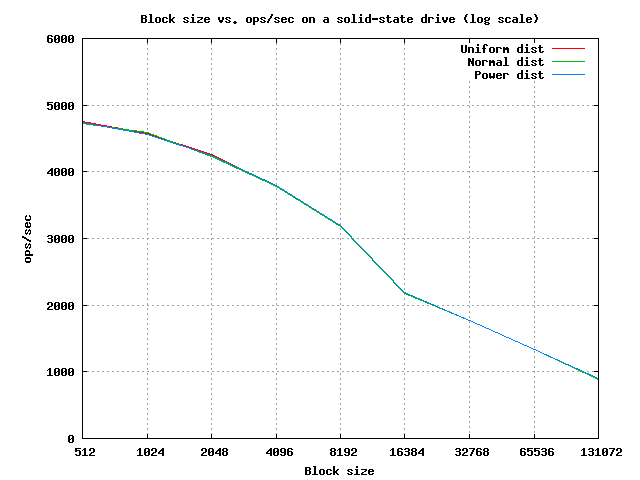
That’s a very different curve! The first thing that jumps out is that random distributions have almost no effect on the results. But what about block size? Given this curve, it isn’t immediately clear what the ideal block size is. Fortunately, we can easily figure it out with a little math. The depth of the B-tree is logb (N) - this is how many hops we need to make to satisfy a given point query.
Let’s perform some back of the envelope calculations for a database of one billion rows. Assuming we can fit a single key into the B-tree node in 32 bytes, we can easily figure out the value of B for each block size. Now, all we need to do is plug in N (we use one billion rows) and B into the formula to figure out how many hops we need to make. We simply divide the number of IOPS for each block size from the experimental data above, and we see how many queries per second we can perform with a given block size. We then pick the block size that lets us perform the maximum number of queries (part of the table removed in the interest of brevity):
| 1kb (32 keys) 4579 IOPS | 2kb (64 keys) 4254 IOPS | 4kb (128 keys) 3780 IOPS | 8kb (256 keys) 3197 IOPS | 16kb (512 keys) 2186 IOPS | 32kb (1024 keys) 1769 IOPS | 64kb (2048 keys) 1334 IOPS |
|---|---|---|---|---|---|---|
| 5.98 hops | 4.98 hops | 4.27 hops | 3.74 hops | 3.32 hops | 2.98 hops | 2.72 hops |
| 765 q./sec | 854 q./sec | 885 q./sec | 854 q./sec | 658 q./sec | 593 q./sec | 490 q./sec |
So, if we have no cache the optimal block size is 4KB.
There are a number of other factors we didn’t consider here. The most important one is caching. A complete analysis would account for the size of the block cache and how many hops we can avoid by storing some of the tree in memory (naturally this is affected by the block size). Another important factor is write performance. Because RethinkDB makes no in-place modifications, we can safely ignore write-heavy workloads - a scenario that can radically affect the calculations above for traditional databases. Finally, we ignore page read boundaries - a factor that can give a significant boost to performance on solid-state drives. More on that later.
Of course, we wouldn’t ask our customers to go through these calculations. RethinkDB will perform these tests on target hardware automatically and suggest the optimal page size, so you never have to guess.
Edit: A few people e-mailed us to let us know that there are some assumptions our computations rely on that weren’t mentioned in the post. For example, B-Tree nodes might not always be full, which might significantly impact the ideal block size. I want to note that we did not intend to say that 4KB blocks are an ideal size on SSDs. The size of the database, the size of the cache, the means by which the data is inserted, and the performance of the drive (given your file system and RAID configuration) are all crucial factors. In order to determine the ideal size it’s necessary to test the performance of the particular hardware and to plug it into a more complete model. Alternatively, you can switch to RethinkDB when it’s ready.
 RethinkDB Team
RethinkDB Team